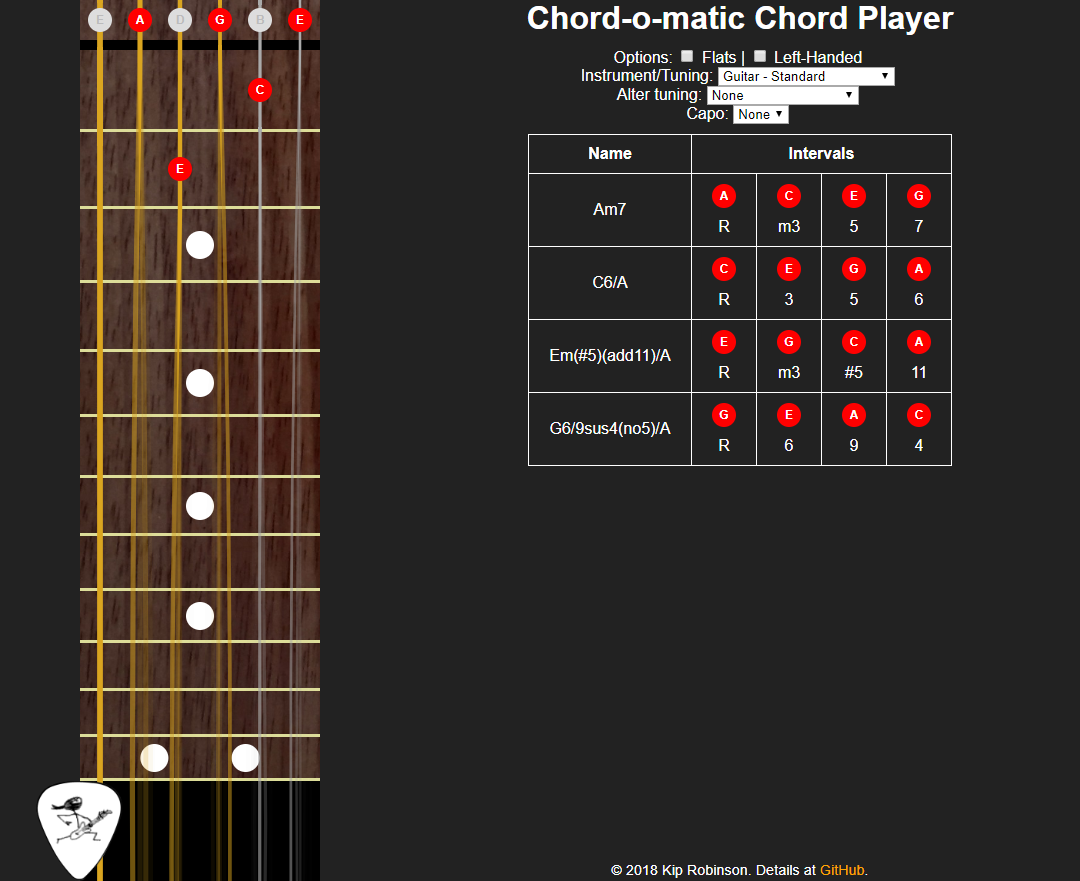
Introducing Chord-o-matic
Warning: I wrote this blog in 2018. That is a long time ago, especially on the internet. My opinions may have changed since then. Technological progress may have made this information completely obsolete. Proceed with caution.
I’ve now released what is quite possibly my most ambitious side project, the Chord-o-matic Chord Player:
This is an app that lets you select the notes that to play on a fretboard, and it tells you possible names for the chord, and why it gave the chord that name. It also lets you hear what the chord will sound like.
My reasons for writing this app come from some frustrations that I have trying to adapt music for guitar. At church, I play guitar for the kids’ choir about every other month, and the music I have to work with is never actually written for guitar. So I start with sheet music that is intended for piano and singing. The problem is I read sheet music at a first grade level. Whereas someone more knowledgeable/experienced than me can just look at the music and say “G, D7, C, G, Am, G7, G” or whatever, I take several hours to get to that point. Usually I start with the sheet music, write down the name of each note, then go back and figure out what chord is being formed by the notes played at that moment. Then I figure out where is the best place to put the capo to play the song more easily.
One tool I found that helped me with this is the JamPlay Guitar Chord Finder, and if you look at that you will see that my app is heavily inspired it. I basically did an HTML5 rewrite of the app. There were a few things that bugged me about their app, and so I set out to change them:
- JamPlay uses Flash, which is quickly going extinct as browser manufacturers drop support for it. I wanted something written in HTML5.
- I needed the option to add a capo, and to alter tuning (i.e. down half step).
- I needed the ability to change the guitar tuning, or even to change the type of instrument (guitar, ukulele, etc.)
Upon setting out, there were two problems I would need to solve:
- The front-end to render the interactive guitar.
- The back-end1 to take a set of pitches and return the possible names of the fingered chord.
I expecteded that the first task would be the most difficult, especially considering my UI skills are not the greatest. But in actuality, I think I spent much more time spinning my wheels on the chord naming task. I assumed that there was some well-defined algorithm which took a set of pitches and returned chord names, and that all I would have to do is open the Wikipedia page or something and port the pseudocode to Javascript. As it turns out, there’s a lot of variation in chord names once you get out of the common chords (majors, minors, and sevenths). Different people have different reasonable interpretations, and many of the established names seem to actively work against any kind of algorithm2. So what I ended up with is a bunch of spaghetti code that I hope to go back to and clean up later, to the extent that it is even possible. One resource that I found extremely helpful for this is the ScalesChords Chord Namer, which lets you select a set of notes in a chord, and it generates possible names for that chord. And, most importantly, it tells you why it generated that particular name. All said and done, I think I learned as much music theory in the past few months as I have in the entire two decades I’ve been playing guitar.
-
Technically, it’s all front-end, but this is the part that’s pure algorithm.
-
For example, you might think a seventh chord is a chord with a seventh in it, but it’s actually one with a flat seventh. A chord with a seventh is called a major seventh. Unless the fifth is flat and you have a minor third (diminished chord), to get a dim7 chord you take a diminished chord and add a double-flat seventh (i.e. sixth) instead of a flat seventh like you do with any other chord. The kind of mess that results in spaghetti code no matter how hard you try.